Sidebar
Part I
The limits of empiricism.
- …
Part II
The gap
- …
Part III
Causes and effects
- …
Part IV
Causal intuitions
- …
This is an old revision of the document!
Table of Contents
Probabilistic vs. Causal inference
This post revisits the confounding phenomenon under the angle of probabilistic reasoning with conditional probabilities and Bayes' theorem. This analysis reveals what sets probabilistic and causal inference apart. It also shows how probabiistic models and causal models formulate assumptions of a fundamentally different nature.
Tip: Feel free to jump to the conclusion if you find this discussion too technical.
Treatments and outcomes
Suppose for instance that we have access to a large trove of medical reports describing the outcomes of applying medical treatment to patients displaying certain symptoms. In the following, we use variable $Y$ to denote observable outcomes such as “patient is considered cured after five days”; we use variable $X$ to denote the treatment selected by a doctor; and we use variable $Z$ to represent the known contextual information. Although we refer to $Z$ as the symptoms variable for simplicity, it really represents all the observed and recorded context of the treatment decision: patient symptoms, patient history, hospital history, place and time, or even environmental factors such as the pollution level.
We merely want to know which treatment $X$ works best for symptoms $Z$.
This question is natural but also ambiguous. Did we mean
- Which treatment $X$ has historically worked best for patients with specific symptoms $Z$, or
- Which treatment $X$ would work best for patients with specific symptoms $Z$?
Confounding exists because these two questions often have different answers.
Conditioning
To answer the first question, we merely need to go through our medical records and count the observed outcomes $Y$ for each symptom-treatment pair $(Z,X)$. If we assume that our records are independent samples from a joint probability distribution $P(Z,X,Y)$, this amounts to estimating the conditional probability distribution $P(Y|Z,X)$.
Since it is very unlikely that our trove of medical reports covers all possible combinations of symptoms $Z$ and treatments $X$ we may have no data to estimate $P(Y|Z,X)$ when $(Z,X)$ is one of these missing pairs. This is not a problem if our goal is merely to answer the first question because saying which treatments have historically worked best does not require us to know anything about treatments we never tried. In contrast, the second question is more demanding because the best treatment for symptoms $Z$ could possibly be a treatment that was never tried for such symptoms. This difference is only the tip of a much larger iceberg.
Interventions
Essentially the second question envisions an intervention to change the treatment selection policy. Instead of doing whatever the doctors were doing to select a treatment during the data collection period, we are considering an alternate treatment selection policy and we would like to know about its performance.
We can approach such an intervention by decomposing the joint distribution as \begin{equation} \label{eq:xyz} P(Z,X,Y) = P(Z) \, P(X|Z) \, P(Y|Z,X)~. \end{equation} This particular ordering of the variables is attractive because it obeys the arrow of time: first come the symptoms with distribution $P(Z)$, then comes the treatment selection with distribution $P(X|Z)$, and finally comes the treatment outcome with distribution $P(Y|X,Z)$.
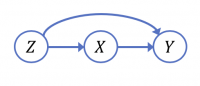 Graphical representation[1] of the decomposition \eqref{eq:xyz}.
Graphical representation[1] of the decomposition \eqref{eq:xyz}.
Each node in this graph represents one variable and receives arrows from all
variables that condition the corresponding term in the decomposition.
We would like to know how our medical records would look like if we were to follow an alternate policy to select a treatment $X$ given symptoms $Z$. This calls for replacing the term $P(X|Z)$ in the decomposition \eqref{eq:xyz} by a new conditional distribution $\textcolor{red}{P^*(X|Z)}$ that represents the alternate treatment selection policy. \begin{equation} \label{eq:xyz:interv} \textcolor{red}{P^*(Z,X,Y)} = P(Z) \, \textcolor{red}{P^*(X|Z)} \, P(Y|Z,X)~. \end{equation}
Does the new joint distribution $\textcolor{red}{P^*(Z,X,Y)}$ represents what one could observe if one were to implement the new treatment policy? Equivalently, do the conditional distributions $P(Z)$ and $P(Y|Z,X)$ remain invariant when one changes the treatment policy $P(X|Z)$.
Nontrivial assumption: Changing the treatment selection policy in decomposition \eqref{eq:xyz} leaves the terms $P(Z)$ and $P(Y|Z,X)$ invariant.
Such an assumption is not a part of our probabilistic model of the data, namely the assumption that the medical records were independently sampled from a joint distribution $P(Z,X,Y)$. To determine whether this assumption is correct or not, we must invoke pieces of knowledge that do not change the probabilistic model itself. These pieces of knowledge are often formulated in causal terms:
- The distribution of symptoms $P(Z)$ could be changed by causal factors beyond our control such as the appearance of new viral strains. We can avoid such difficulties by reformulating our question with a different tense : which treatment selection policy would have worked best if it had been applied to the cases described in our trove of medical records? This is called a counterfactual question because it pertains to something that did not happen and cannot happen anymore. Since this question it applies to past cases, the unobserved environmental factors can be assumed to remain identical. Meanwhile, answering this counterfactual question still provides useful knowledge.
- Since the symptoms are observed before the treatment selection, we can argue that the changing the treatment cannot change the symptoms. In the context of the counterfactual question, this means that their distribution $P(Z)$ is not affected by changes to the treatment selection policy $P(X|Z)$.
- The invariance of the conditional outcome distribution $P(Y|Z,X)$ is harder to justify. For instance, we may believe that the outcome $Y$ is a deterministic function of the observed symptoms $Z$, the selected treatments $X$, and, possibly, an independent roll of the dices. But what to conclude if we believe instead that the outcome could depend on symptoms that were not observed or not recorded in the medical records?
Unobserved variables
Probabilities are often used to represent processed that we cannot model completely. For instance, what happens when we roll the dices might depend on their initial configuration, the speed of our motion, the exact moment we release the dices, the temperature of the air, etc. Since we do not know these things, we simply say that each face of a dice is shown with equal chance.
We shall now change our model to include a new variable $U$ that represents additional information that was not recorded in the medical reports and therefore is no longer accessible. The exact nature of the information $U$ is not important at this point, except for the fact that it may impact which treatment was applied as well as its outcome. Such a variable $U$ is often called an unobserved variable because its value is unknown at the time of the analysis of the data.
Interventions in the presence of unobserved variables
The canonical decomposition then becomes \begin{equation} \label{eq:xyzu} P(Z,U,X,Y) = P(Z) \, P(U|Z) \, P(X|Z,U) \, P(Y|X,Z,U) ~. \end{equation}
We can then write the observed joint distribution $P(Z,X,Y)$ as \begin{align*} P(Z,X,Y) &= \sum_U P(Z,U,X,Y) \\ &= P(Z) \, \sum_U P(U|Z) \, P(X|U,Z) \, P(Y|X,U,Z)~. \end{align*}
The term $P(X|Z,U)$ that represents which treatments $X$ were applied now depends on both the symptoms $Z$ and the unobserved variable $U$. Proceeding as in the previous section, we replace this term by the conditional distribution $\textcolor{red}{P^*(X|Z)}$ that represents an alternate treatment policy. Note that the alternate policy cannot depend on $U$ because we do not know $U$. This gives the following expression for the alternate joint distribution \begin{equation} \label{eq:xyzu:interv} \textcolor{red}{P^*(Z,X,Y)} = P(Z) \, \textcolor{red}{P^*(X|Z)} ~ \textcolor{blue}{\underbrace{\sum_U P(U|Z) \, P(Y|Z,X,U)}_{P^*(Y|Z,X)} } \end{equation}
New assumption: We now assume here that changing the treatment policy leaves the terms $P(Z)$, $P(U|Z)$, and $P(Y|Z,X,U)$ invariant.
The nature of this new assumption depends of course on the assumed nature of the unobserved variable $U$. For instance, if the variable $U$ is constant, our new assumption is equivalent to our previous assumption, namely the invariance of $P(Z)$ and $P(Y|Z,X)$. We now would like to know whether there are choices of $U$ that make this assumption different and lead to different conclusions.
This boils down to determining whether the blue term in \eqref{eq:xyzu:interv} \[ \textcolor{blue}{P^*(Y|Z,X) = \sum_U P(U|Z) P(Y|Z,X,U) } ~, \] is equal to \[ P(Y|Z,X) = \sum_U P(Y,U|Z,X) = \sum_U P(U|Z,X) P(Y|Z,X,U) \] If these terms were equal, expressions \eqref{eq:xyzu:interv} and \eqref{eq:xyz:interv} would be identical and therefore would lead to the same conclusions regardless of the nature of the unknown information $U$. Unfortunately the first expression has $P(U|Z)$ where the second expression has $P(U|Z,X)$.
These two conditional distribution are nevertheless equal in two important cases:
- when the unobserved variable $U$ has no impact on the outcomes,that is, when $P(Y|Z,X,U)=P(Y|Z,X)$, and
- when the unobserved variable $U$ had no impact on the selected treatments, that is, when $P(X|Z,U)=P(X|Z)$.
Proof: In the first case, we can indeed write \[ P^*(Y|Z,X) = \sum_U P(U|Z) P(Y|Z,X,U) = \big( \sum_U P(U|Z) \big) P(Y|Z,X) = P(Y|Z,X)~. \] For the second case, decomposing $P(X,U|Z)$ in two ways, \[ P(X,U|Z) = P(X|Z) P(U|Z,X) = P(U|Z) P(X|Z,U)~, \] shows that $P(X|Z,U){=}P(X|Z) \Longleftrightarrow P(U|Z){=}P(U|Z,X)$. Therefore $P^*(Y|Z,X){=}P(Y|Z,X)$. $~\blacksquare$
However, when the unobserved variable $U$ impacts both the treatments and the outcomes, the two conditional distributions $\textcolor{blue}{P^*(Y|Z,X)}$ and $P(Y|Z,X)$ are not equal. Since equations \eqref{eq:xyz:interv} and \eqref{eq:xyzu:interv} are different, it is very likely that these two approaches lead to different joint distributions $\textcolor{red}{P^*(Z,X,Y)}$ and therefore different conclusions about which treatment works best for which symptom. To make things worse, we cannot in general estimate $\textcolor{blue}{P^*(Y|Z,X)}$ as defined in equation \eqref{eq:xyzu:interv} because it depends on the unobserved variable $U$ which cannot be found in our medical records.
Conclusion
This example illustrates a fundamental difference between probabilistic and causal inference.
- Probabilistic inference: Knowing the joint distribution of the observed variables is enough to compute all the conditional distributions and therefore sufficient to answer any probabilistic inference question pertaining to the observed variablers.
- Causal inference: Knowing the joint distribution of the observed variables is generally not sufficient to answer a causal inference question pertaining to the observed variable: the outcome of interventions on the observed variables potentially depends on unobserved parts of the system.
This also implies that probabilistic and causal modeling are fundamentally different
- Probabilistic models make it easier to estimate the joint distribution of the observed variable. Making conditional independence assumptions or making parametric assumptions helps us to produce an estimate using only a limited number of examples.
- Causal models potentially make it possible to estimate the outcome of interventions. We simply cannot give an answer without making invariance assumptions or making independence assumption with respect to unobserved quantities.