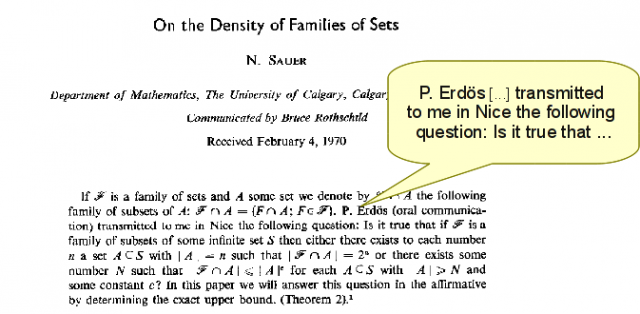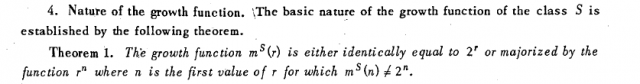On the Vapnik-Chevonenkis-Sauer lemma

Many machine learning authors write that a certain fundamental combinatorial result was independently established by Vapnik and Chervonenkis (1971), Sauer (1972), Shelah (1972), and sometimes Perles and Shelah (reference unknown). Vapnik and Chervonenkis published a version of their results in the Proceedings of the USSR Academy of Sciences four years earlier in 1968. It also appears that Sauer and Shelah pursued this result for very different purposes.

Since the lemma is most often attributed to Sauer, let us first have a closer look at Sauer's 1972 paper. The paper provides a set theoretical statement of the lemma and proves it by induction. However the most curious part of the paper is its motivation: “P. Erdös transmitted to me in Nice the following question: is it true that <insert lemma here>”.

The first surprising thing is that Sauer's paper contains no further motivation for the lemma. The second surprising thing is that Sauer does not even attributes the conjecture to Erdös. There is no doubt that a question from Erdös himself carries some weight. However a conjecture from Erdös would have carried more weight than a simple question.

When exactly did Erdös ask the question? Sauer casually mentions Nice with the apparent expectation that everyone understands what he is referring to. This clearly points to the International Congress of Mathematicians held in Nice on September 1--10, 1970. However, there is an inconsistency because the final version of the paper, published in July 1972, bears the mention ``received in February 1970'', that is, before the Nice congress. Does it mean that Sauer's paper substantially evolved during the review period or does it mean that Sauer and Erdös met in Nice months before the Nice congress? The question has an importance because it has been argued that the mention “received in February 1970” suggests that Sauer's work predates Vapnik and Chervonenkis (1971).

Finally, supporting the possibility that the paper evolved significantly during the review period, Sauer writes that a referee pointed out how Shelah had proven similar results in two papers awaiting publication. The final versions of these papers were also published in 1972. Although I have read them, I am unable to determine whether they contain a version of the lemma. I am not alone: E. Kowalski writes that “whereas it is easy to find the result in the paper of Vapnik-Chernovenkis, (he) would be hard put to give a precise location in Shelah’s paper where he actually states this dichotomy”, and J. M. Steele writes that he “could not see (his) way to it through the thicket of mathematical logic”. Richard M. Dudley pointed out that this result appears in Definition 1.5 of Shelah's 1972 paper. He can obviously read better than I can!

Shelah's papers however reveal why mathematicians as eminent as Erdös and his entourage had an interest in this result: the lemma describes how infinite sets appear when one observes them through a finite number of predicates. This has potential implications for set theory and mathematical logic foundations. This is certainly not statistical learning theory as we know it.

Most machine learning papers mentionning Sauer's 1972 lemma are in fact discussing the statistical learning framework pionneered by Vapnik and Chervonenkis. Many authors recognize that they have learned about the lemma and about its purpose from the english translation of the Vapnik and Chervonenkis 1971 paper.

The above picture is in fact the russian version of the paper. The last page contains the references and an english summary.

Two little details should catch our attention. The first one is the mention “received for review in May 1969”. This is clearly before the submission of Sauer's paper in February 1970, which may or may not have contained the lemma in its current form. Of course we do not know at this point how complete was the first version of the Vapnik and Chervonenkis paper. The second detail is the citation of an earlier paper published in 1968 in the Proceedings of the USSR Academy of Sciences.

It turns out that the American Mathematical Society published an English translation of this particular issue of Proceedings of the USSR Academy of Sciences the same year (1968).

In fact, this is a lovely short paper. In four pages, the paper describes the three main results of the Vapnik-Chervonenkis theory and explains that they are important for “the construction of learning algorithms.”. This is already a well developed work.

The lemma appears as Theorem 1, given without proof because of space constraints.

Shortly after the publication of this paper, R. M. Dudley wrote for Mathematical Reviews that “very interesting results” had been are announced. V. Vapnik told me that this review was instrumental in obtaining the permission to publish the full paper. It is easy to imagine Erdös reading about this result given without proof by two relatively unknown scientists, wondering whether the result is true, and whether it could be applied with even greater impact to set theory and to the foundation of mathematics. It is however likely that Erdös did not have the proof when he asked Sauer in 1970. It is also likely that Vapnik and Chervonenkis had the proof in 1968 and most certainly had submitted in with their longer paper in 1969.

In a recent email, R. M. Dudley points out a difference between the various versions of the lemma:

When \( \displaystyle n \ge h\,,\) where h denotes the Vapnik-Chervonenkis dimension of S,

• Vapnik and Chervonenkis (1971) prove that \(\displaystyle m_S(n) < \sum_{k=0}^{h} \left(\begin{array}{cc} n \\ k \end{array}\right) . \)
• Sauer (1972) proves that \(\displaystyle m_S(n) \le \sum_{k=0}^{h-1} \left(\begin{array}{cc} n \\ k \end{array}\right) , \) which is a tighter result.

Although this difference exists, it has minimal impact on learning theory. It does not make the original Vapnik-Chervonenkis bounds usable for practical machine learning (one needs data-dependent and algorithm-dependent results for this). In fact both bounds are proven using the same methods, which generalize existing bound on the number of dichotomies achievable with linear separators (Cover, 1964), which is in fact tighter than both. The subsequent book (Vapnik and Chervonenkis, 1974) gives an updated discussion with a linear case bound similar to Cover's and a general case bound similar to Sauer's. However they do not seem to have been aware of Sauer's tighter result.

I eventually realized that Norbert Sauer is not just a printed name on an old paper. Finding him took only a Google search. He replied very kindly to my nosy questions:

“When I proved that Lemma, I was very young and have since moved my interest more towards model theoretic type questions. As far as I can remember, Erdös visited Calgary and told me at that occasion that this question has come up. But I do not remember the context in which he claimed that it did come up. I then produced a proof and submitted it as a paper. I did not know about that question before the visit by Erdös. I found the proof quite soon, a few weeks at most, after the visit by Erdös.”

So it started in Calgary. Maybe they talked about it again in Nice…

• T. Cover (1964): Geometrical and Statistical Properties of Linear Threshold Devices. Ph.D. Thesis, Stanford.

• N. Sauer (1972): On the density of families of sets. J. Combinatorial Theory Ser. A 13, July 1972, 145–147.

• S. Shelah (1972): A combinatorial problem; stability and order for models and theories in infinitary languages. Pacific J. Math. 41, 247–261.

• V. N. Vapnik, A. Ya. Chervonenkis (1968): On the uniform convergence of relative frequencies of events to their probabilities, Soviet Math. Dokl., 9, 915-918. English translation of “О равномерной сходимости частот появления событий к их вероятностям”, Доклады Академии Наук СССР, 181, 4 (1968), 781.

• V. N. Vapnik, A. Ya. Chervonenkis (1971): On the uniform convergence of relative frequencies of events to their probabilities. Theory of Probability and its Applications 16(2), 264—281.

• V. N. Vapnik, and A. Ya. Chervonenkis, (1974). Теория распознавания образов [Theory of pattern recognition]. Nauka.