Sidebar
Part I
The limits of empiricism.
- …
Part II
The gap
- …
Part III
Causes and effects
- …
Part IV
Causal intuitions
- …
Table of Contents
Confounding
This post presents and comments a classic example of confounding variable in real life. The intricacies of the phenomenon and their relation to Bayes'rule are discussed in a second post).
Kidney stones
Kidney stones are hard mineral deposits that form inside the kidneys, can lodge themselves in annoying locations of the urinary tract, become very painful, and may have to be removed. A 1986 study[1] compares the outcomes of a variety of stone removal treatments performed between 1972 and 1985 in a group of London hospitals.
- Extracorporeal shockwave lithotripsy (ESWL) uses ultrasounds to break the stones in small pieces that can be evacuated by urination. This was a relatively new treatment in 1986. Although the study concludes that this is the best treatment option, we are going to focus on the next two options.
- Percutaneous Nephrolithotomy (PCNL) is a form of keyhole surgery. Kidney stones are extracted using a telescopic instrument introduced through a small incision in the skin.
- Open surgery covers several surgical procedures in which a surgeon exposes the kidney and removes or breaks the stones. These are comparatively heavy procedure with all the potential complications of a major surgery.
Between 1972 and 1985, two groups of 350 patients were respectively treated with open surgery and PCNL. Table 1 shows the overall success rates observed for these two groups, suggesting that PCNL is a far better option because it has a higher success rate and less potential for complications.
Table 1 – Overall success rates of open surgery and PCNL.
| Treatement | Overall sucess |
|---|---|
| Open Surgery | 78% (273/350) |
| PCNL | 83% (289/350) |
It turns out that this conclusion is not completely accurate because doctors tried to avoid open surgery and its potential complication except for patients with very large stones. Therefore, during the study period, PCNL was applied to comparatively easier cases. Table 2 breaks down the success rates of both treatments according to the stone size.
Table 2 – Success rates broken down by stone sizes.
| Treatement | Overall sucess | Small stones | Large stones |
|---|---|---|---|
| Open Surgery | 78% (273/350) | 93% (81/87) | 73% (192/263) |
| PCNL | 83% (289/350) | 87% (234/270) | 69% (55/80) |
This new table reveals that open surgery was a more successful treatment for both small and large stones. The apparent superiority of PCNL was merely an illusion that arose from being disproportionately applied to patients with less severe conditions.
This change has practical consequences for doctors facing a choice between open surgery and PCNL. Instead of systematically opting for PCNL, doctors must now weigh the increased risk of complications versus the better success rates of open surgery. Reassuringly, this also means that choosing to only use surgery for the most serious case was a sensible choice. Nowadays, doctors are more likely to select the more modern ultra-sound technique (ESWL) which was found to have both the highest success rates and the least complications.
The effect illustrated by Tables 1 and 2 is called Simpson's paradox[2]. This simply means that one can easily reach the wrong conclusion when one fails to take into account all variables that potentially affect both the selection of a treatment and its outcome. This sets a serious problem because it is often difficult to build a list of all these potentially confounding variables.
Invariants and decisions
We must however clarify a last point: we have seen that these tables lead to different conclusions, but we have not precisely explained why we believe Table 2 over Table 1! Although this seems very natural, giving a precise explanation is surprisingly involved.
We can explain this preference with the following assumption:
The success of the procedure is a function of the condition of the patient and of the nature of the procedure. This function remains invariant to changes in the distribution of the patient conditions or in the decision processes that lead to the selection of a procedure.
For instance, we may specialize in patients with nutritional problems, and doctors may select a procedure by tossing a coin instead of a thorough analysis. Both these changes would affect the joint distribution of patient conditions and procedures. But we assume that these changes would not affect the function that tells the outcome given the patient condition and the nature of the procedure.
This assumption clarifies the nature of the conclusion we are seeking. We are in fact trying to acquire enough knowledge about this invariant function to predict the effects of an intervention such as changing the treatment selection policy. What would be the overall success rate if we were to always use surgery? or always use PCNL? or use surgery for small stones and PCNL for large stones?
Note that we can only observe a subset of the arguments of the invariant function. For instance we do not know whether the patient has some yet-undiscovered pathology. Therefore we can only understand how this function depends on the observed variables and treat the unobserved variables as independent noise. Table 1 tells us how the average value of the function depends on a single variable, namely the selected treatment. Table 2 reveals that the stone size cannot be treated as independent noise: there is indeed a dependence between the stone size and the selected treatment. Therefore we conclude that Table 2 is closer to the truth.
Randomized experiments
Alas it is very hard to be certain that all the potential confounding variables have been taken into account. Take for instance the availability of an experienced surgeon. This variable could easily have affected the treatment decision, and could certainly affect the quality of the surgery and its outcome. Would our conclusion be again reversed if we could take this variable into account? We have no way to know…
We cannot answer such questions with certainty without taking full control of the treatment selection policy during the study in order to limit which variables can affect the choice of a treatment. This is achieved by selecting a treatment at random, –that is, with an independent roll of the dices,– according to a distribution that only depends on a few chosen observed variables.[3] [4] Since a confounding variable must impact both the treatment and the outcome, we only need to take into account those few chosen variables in the analysis. Under such conditions, no other variable, observed or not, can confound our conclusions.
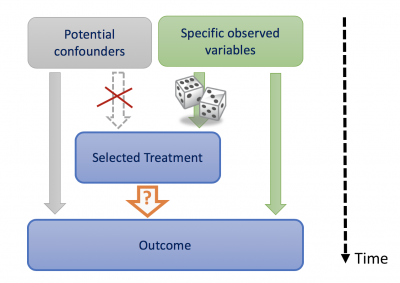 Figure 3 – Randomization ensures that the selected treatment only depends on specific observed variables. Therefore no other variable can be confounding.
Figure 3 – Randomization ensures that the selected treatment only depends on specific observed variables. Therefore no other variable can be confounding.
This full control requirement sets a very high bar for experiments. Can we prevent doctors to do what they believe is best for their patient? Should we refrain from repurposing previously collected data to perform a new analysis? The kidney stone study certainly shows that there often is much to learn from an imperfect experiment.