Large Scale Learning

The methods of conventional statistics were developed in times where both dataset collection and modeling were carried out with paper and pencil. The appearance of computers first displaced the pencil for model calculation. Machine learning gained prominence by exploiting this new opportunity, enabling the construction of efficient high-dimensional models using comparatively small training sets. Another change of similar magnitude is underway. Pervasive and networked computers have reduced the cost of collecting and distributing large-scale datasets. We now need learning algorithms that scale linearly with the volume of the data, while maintaining enough statistical efficiency to outperform algorithms that simply process a random subset of the data.

For the sake of the argument, assume that there are only two categories of computers. The first category, the makers, directly mediate human activity. They implement the dialogue between sellers and buyers, run the accounting department, control industrial processes, route telecommunications, etc. The makers generate and collect huge quantities of data. The second category, the thinkers, analyze this data, build models, and draw conclusions that direct the activity of the makers. Makers produce datasets whose size grows linearly with their collective computing power. We can roughly write this size as n d where n is a number of examples and d the number of features per example. The computational needs of state-of-the-art learning algorithms typically grow like n^2 d or n d^2. If thinkers were to use these algorithms, their collective computing power would have to vastly exceed that of the makers. This is economically infeasible. The Googles of this world cannot deploy vastly more resources than all their customers together: their advertisement income cannot exceed the wealth of those who receive the messages, because the advertisers would never sell enough to recoup their expense.

Hence we need algorithms that scale linearly with the size of the training data.

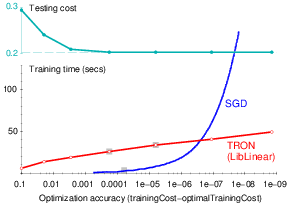Large-scale machine learning was first approached as an engineering problem. For instance, to leverage a larger training set, we can use a parallel computer to run a known machine learning algorithm or adapt more advanced numerical methods to optimize a known machine learning objective function. Such approaches rely on the appealing assumption that one can decouple the statistical aspects from the computational aspects of the machine learning problem.

This work shows that this assumption is incorrect, and that giving it up leads to considerably more effective learning algorithms. A new theoretical framework takes into account the effect of approximate optimization on learning algorithms.

The analysis shows distinct tradeoffs for the case of small-scale and large-scale learning problems. Small-scale learning problems are subject to the usual approximation–estimation tradeoff. Large-scale learning problems are subject to a qualitatively different tradeoff involving the computational complexity of the underlying optimization algorithms in non-trivial ways. For instance, Stochastic Gradient Descent (SGD) algorithms appear to be mediocre optimization algorithms and yet are shown to perform extremely well on large-scale learning problems.

• NIPS 2007 tutorial “Large Scale Learning”.

• Stochastic gradient learning algorithms